Public And Private Keys Rsa Key Generation
- Jun 22, 2012 SSH keys provide a more secure way of logging into a virtual private server with SSH than using a password alone. With SSH keys, users can log into a server without a password. This tutorial explains how to generate, use, and upload an SSH Key Pair.
- Public-key cryptography, or asymmetric cryptography, is a cryptographic system that uses pairs of keys: public keys, which may be disseminated widely, and private keys,which are known only to the owner.
- Generate RSA key pair and encode private as string. I want to generate 512 bit RSA keypair and then encode my public key as a string. RSA 512 bit keys are.
- No, RSA encryption with a private key is not the same as RSA signature generation. RSA encryption can only be performed with an RSA public key according to the RSA standard. The terms Raw RSA or textbook RSA are often used to indicate RSA without a padding scheme. Raw RSA simply consists of modular exponentiation.
- Now the plan is to store the private key xml on a USB drive attached to the managers key chain. Whenever a manager leaves the company I want to be able to generate new public and private keys (and re-encrypt all currently stored CC numbers with the new public key). My problem is that the keys generated by this code are always the same.
- Public And Private Keys Rsa Key Generation Review
- Public And Private Keys Rsa Key Generation Linux
- Public And Private Keys Rsa Key Generation Example
- Cryptography Tutorial
- Cryptography Useful Resources
Generating Public/Private RSA Keys What are Public and Private Keys? Public and private keys are a method of user authentication that is prevalent in the field of server administration. They keys themselves are based on a security design referred to as Public Key Cryptography (PKC). Nov 01, 2019 To create a DKIM record you need to generate the public and private keys and allocate them properly. Explore the details in this blog post. Sending and receiving servers must support the rsa key type, which indicates that an ASN.1 DER-encoded public key is being used in the p= tag.
- Selected Reading
Public Key Cryptography
Unlike symmetric key cryptography, we do not find historical use of public-key cryptography. It is a relatively new concept.
Symmetric cryptography was well suited for organizations such as governments, military, and big financial corporations were involved in the classified communication.
With the spread of more unsecure computer networks in last few decades, a genuine need was felt to use cryptography at larger scale. The symmetric key was found to be non-practical due to challenges it faced for key management. This gave rise to the public key cryptosystems.
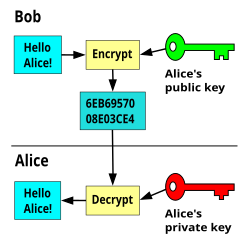
The process of encryption and decryption is depicted in the following illustration −
The most important properties of public key encryption scheme are −

Different keys are used for encryption and decryption. This is a property which set this scheme different than symmetric encryption scheme.
Each receiver possesses a unique decryption key, generally referred to as his private key.
Receiver needs to publish an encryption key, referred to as his public key.
Some assurance of the authenticity of a public key is needed in this scheme to avoid spoofing by adversary as the receiver. Generally, this type of cryptosystem involves trusted third party which certifies that a particular public key belongs to a specific person or entity only.
Encryption algorithm is complex enough to prohibit attacker from deducing the plaintext from the ciphertext and the encryption (public) key.
Though private and public keys are related mathematically, it is not be feasible to calculate the private key from the public key. In fact, intelligent part of any public-key cryptosystem is in designing a relationship between two keys.
There are three types of Public Key Encryption schemes. We discuss them in following sections −
RSA Cryptosystem
This cryptosystem is one the initial system. It remains most employed cryptosystem even today. The system was invented by three scholars Ron Rivest, Adi Shamir, and Len Adleman and hence, it is termed as RSA cryptosystem.
Windows server 2012 generate ssh key. We will see two aspects of the RSA cryptosystem, firstly generation of key pair and secondly encryption-decryption algorithms.
Generation of RSA Key Pair
Each person or a party who desires to participate in communication using encryption needs to generate a pair of keys, namely public key and private key. The process followed in the generation of keys is described below −
Generate the RSA modulus (n)
Select two large primes, p and q.
Calculate n=p*q. For strong unbreakable encryption, let n be a large number, typically a minimum of 512 bits.
Find Derived Number (e)
Number e must be greater than 1 and less than (p − 1)(q − 1).
There must be no common factor for e and (p − 1)(q − 1) except for 1. In other words two numbers e and (p – 1)(q – 1) are coprime.
Form the public key
The pair of numbers (n, e) form the RSA public key and is made public.
Interestingly, though n is part of the public key, difficulty in factorizing a large prime number ensures that attacker cannot find in finite time the two primes (p & q) used to obtain n. This is strength of RSA.
Generate the private key
Private Key d is calculated from p, q, and e. For given n and e, there is unique number d.
Number d is the inverse of e modulo (p - 1)(q – 1). This means that d is the number less than (p - 1)(q - 1) such that when multiplied by e, it is equal to 1 modulo (p - 1)(q - 1).
This relationship is written mathematically as follows −
The Extended Euclidean Algorithm takes p, q, and e as input and gives d as output.
Example
An example of generating RSA Key pair is given below. (For ease of understanding, the primes p & q taken here are small values. Practically, these values are very high).
Let two primes be p = 7 and q = 13. Thus, modulus n = pq = 7 x 13 = 91.
Select e = 5, which is a valid choice since there is no number that is common factor of 5 and (p − 1)(q − 1) = 6 × 12 = 72, except for 1.
The pair of numbers (n, e) = (91, 5) forms the public key and can be made available to anyone whom we wish to be able to send us encrypted messages.
Input p = 7, q = 13, and e = 5 to the Extended Euclidean Algorithm. The output will be d = 29.
Check that the d calculated is correct by computing −
Hence, public key is (91, 5) and private keys is (91, 29).
Encryption and Decryption
Once the key pair has been generated, the process of encryption and decryption are relatively straightforward and computationally easy.
Interestingly, RSA does not directly operate on strings of bits as in case of symmetric key encryption. It operates on numbers modulo n. Hence, it is necessary to represent the plaintext as a series of numbers less than n.
RSA Encryption
Suppose the sender wish to send some text message to someone whose public key is (n, e).
The sender then represents the plaintext as a series of numbers less than n.
To encrypt the first plaintext P, which is a number modulo n. The encryption process is simple mathematical step as −
In other words, the ciphertext C is equal to the plaintext P multiplied by itself e times and then reduced modulo n. This means that C is also a number less than n.
Returning to our Key Generation example with plaintext P = 10, we get ciphertext C −
RSA Decryption
The decryption process for RSA is also very straightforward. Suppose that the receiver of public-key pair (n, e) has received a ciphertext C.
Receiver raises C to the power of his private key d. The result modulo n will be the plaintext P.
Returning again to our numerical example, the ciphertext C = 82 would get decrypted to number 10 using private key 29 −
RSA Analysis
The security of RSA depends on the strengths of two separate functions. The RSA cryptosystem is most popular public-key cryptosystem strength of which is based on the practical difficulty of factoring the very large numbers.
Encryption Function − It is considered as a one-way function of converting plaintext into ciphertext and it can be reversed only with the knowledge of private key d.
Key Generation − The difficulty of determining a private key from an RSA public key is equivalent to factoring the modulus n. An attacker thus cannot use knowledge of an RSA public key to determine an RSA private key unless he can factor n. It is also a one way function, going from p & q values to modulus n is easy but reverse is not possible.
If either of these two functions are proved non one-way, then RSA will be broken. In fact, if a technique for factoring efficiently is developed then RSA will no longer be safe.
The strength of RSA encryption drastically goes down against attacks if the number p and q are not large primes and/ or chosen public key e is a small number.
ElGamal Cryptosystem
Along with RSA, there are other public-key cryptosystems proposed. Many of them are based on different versions of the Discrete Logarithm Problem.
ElGamal cryptosystem, called Elliptic Curve Variant, is based on the Discrete Logarithm Problem. It derives the strength from the assumption that the discrete logarithms cannot be found in practical time frame for a given number, while the inverse operation of the power can be computed efficiently.
Let us go through a simple version of ElGamal that works with numbers modulo p. In the case of elliptic curve variants, it is based on quite different number systems.
Generation of ElGamal Key Pair
Each user of ElGamal cryptosystem generates the key pair through as follows −
Choosing a large prime p. Generally a prime number of 1024 to 2048 bits length is chosen.
Choosing a generator element g.
This number must be between 1 and p − 1, but cannot be any number.
It is a generator of the multiplicative group of integers modulo p. This means for every integer m co-prime to p, there is an integer k such that gk=a mod n.
For example, 3 is generator of group 5 (Z5 = {1, 2, 3, 4}).
| N | 3n | 3n mod 5 |
|---|---|---|
| 1 | 3 | 3 |
| 2 | 9 | 4 |
| 3 | 27 | 2 |
| 4 | 81 | 1 |
Choosing the private key. The private key x is any number bigger than 1 and smaller than p−1.
Computing part of the public key. The value y is computed from the parameters p, g and the private key x as follows −
Obtaining Public key. The ElGamal public key consists of the three parameters (p, g, y).
For example, suppose that p = 17 and that g = 6 (It can be confirmed that 6 is a generator of group Z17). The private key x can be any number bigger than 1 and smaller than 71, so we choose x = 5. The value y is then computed as follows −
Thus the private key is 62 and the public key is (17, 6, 7).
Encryption and Decryption
The generation of an ElGamal key pair is comparatively simpler than the equivalent process for RSA. But the encryption and decryption are slightly more complex than RSA.
ElGamal Encryption
Suppose sender wishes to send a plaintext to someone whose ElGamal public key is (p, g, y), then −
Sender represents the plaintext as a series of numbers modulo p.
To encrypt the first plaintext P, which is represented as a number modulo p. The encryption process to obtain the ciphertext C is as follows −
- Randomly generate a number k;
- Compute two values C1 and C2, where −
Send the ciphertext C, consisting of the two separate values (C1, C2), sent together.
Referring to our ElGamal key generation example given above, the plaintext P = 13 is encrypted as follows −
- Randomly generate a number, say k = 10
- Compute the two values C1 and C2, where −
Send the ciphertext C = (C1, C2) = (15, 9).
ElGamal Decryption
To decrypt the ciphertext (C1, C2) using private key x, the following two steps are taken −
Compute the modular inverse of (C1)x modulo p, which is (C1)-x , generally referred to as decryption factor.
Obtain the plaintext by using the following formula −
In our example, to decrypt the ciphertext C = (C1, C2) = (15, 9) using private key x = 5, the decryption factor is
Extract plaintext P = (9 × 9) mod 17 = 13.
ElGamal Analysis
Public And Private Keys Rsa Key Generation Review
In ElGamal system, each user has a private key x. and has three components of public key − prime modulus p, generator g, and public Y = gx mod p. The strength of the ElGamal is based on the difficulty of discrete logarithm problem.
The secure key size is generally > 1024 bits. Today even 2048 bits long key are used. On the processing speed front, Elgamal is quite slow, it is used mainly for key authentication protocols. Due to higher processing efficiency, Elliptic Curve variants of ElGamal are becoming increasingly popular.
Elliptic Curve Cryptography (ECC)
Elliptic Curve Cryptography (ECC) is a term used to describe a suite of cryptographic tools and protocols whose security is based on special versions of the discrete logarithm problem. It does not use numbers modulo p.
ECC is based on sets of numbers that are associated with mathematical objects called elliptic curves. There are rules for adding and computing multiples of these numbers, just as there are for numbers modulo p.
ECC includes a variants of many cryptographic schemes that were initially designed for modular numbers such as ElGamal encryption and Digital Signature Algorithm.
It is believed that the discrete logarithm problem is much harder when applied to points on an elliptic curve. This prompts switching from numbers modulo p to points on an elliptic curve. Also an equivalent security level can be obtained with shorter keys if we use elliptic curve-based variants.
The shorter keys result in two benefits −
- Ease of key management
- Efficient computation
These benefits make elliptic-curve-based variants of encryption scheme highly attractive for application where computing resources are constrained.
RSA and ElGamal Schemes – A Comparison
Let us briefly compare the RSA and ElGamal schemes on the various aspects.
| RSA | ElGamal |
|---|---|
| It is more efficient for encryption. | It is more efficient for decryption. |
| It is less efficient for decryption. | It is more efficient for decryption. |
| For a particular security level, lengthy keys are required in RSA. | For the same level of security, very short keys are required. |
| It is widely accepted and used. | It is new and not very popular in market. |
Generate RSA keys with SSH by using PuTTYgen
One effective way of securing SSH access to your cloud server is to usea public-private key pair. This means that a public key is placed onthe server and a private key is placed on your local workstation.Using a key pair makes it impossible for someone to log in by using justa password, as long as you set up SSH to deny password-basedauthentication.
This article provides steps for generating RSA keys by using PuTTYgen onWindows for secure SSH authentication with OpenSSH.
Generate keys
In Windows, use PuTTYgen to generate your public and private keys.
- If needed, download PuTTYgen from the PuTTY download page.(PuTTYgen might have been installed previously with PuTTY or WinSCP.)
- Launch the program, and then click the Generate button.The program generates the keys for you.
- Enter a unique key passphrase in the Key passphrase andConfirm passphrase fields.For additional information about using passphrases,see Log in with a SSH Private Key on Windows.
- Save the public and private keys by clicking the Save public keyand Save private key buttons.
- From the Public key for pasting into OpenSSH authorized_keys filefield at the top of the window, copy all the text (starting with ssh-rsa)to your clipboard by pressing Ctrl-C.You need this key available on your clipboard to paste eitherinto the public key tool in the Control Panel or directly into theauthorized keys on your cloud server.
Use the key pair
You can use the RSA key pair in the following ways.
Specify your SSH key when creating a new cloud server
When you create a cloud server, you can assign a public key from the list of keys.If your key is not already in the list, you may add it, and then assign it.
Add a new public key to the list
- Under Advanced Options on the Create Server page, click Manage SSHKeys.
- Select public key for the cloud server from the SSH Keys listand click Add Public Key.
- Enter the key name, select the region, and paste the entire publickey into the Public Key field. Then click Add Public Key.
- Go back to the Create Server page, and confirm that your key is listedin the SSH Key list.
Assign a public key
- Under Advanced Options on the Create Server page, select the publickey you want to use from the SSH key drop-down menu.
- When you are done specifying the all the other details for the server,click Create Server.
Assign your SSH Key to an existing cloud server
To make use of your newly generated RSA key pair, you must tell PuTTY touse it when connecting to your cloud server.
To edit the file (or create it), run the following command on the cloud server:
Paste the text onto its own line in the file.
You must have the key available in your clipboard to paste it. The key and itsassociated text (the ssh-rsa identified at the start and the comment at the end)must be on one line in the file. If the text is word-wrapped onto multiple linesan error might occur when connecting.
If you created the authorized_keys file, change its permissionsafter you’re done editing it by running the following command:
Open PuTTY, and go to the SSH > Auth section.
Browse to the location of the key file, and load the private key.
Go to the Session page, and save the session. This saves the configurationso that PuTTY uses the key every time that you connect to your cloudserver.
After you save your session, your key is loaded automatically when youconnect to your server.
Related article
Experience what Rackspace has to offer.
Public And Private Keys Rsa Key Generation Linux
©2020 Rackspace US, Inc.
Public And Private Keys Rsa Key Generation Example
Except where otherwise noted, content on this site is licensed under a Creative Commons Attribution-NonCommercial-NoDerivs 3.0 Unported License