Because of this, a public key can be freely shared. The private key however belongs to only one person. There are several well-known mathematical algorithms that are used to produce the public and private key. Some well-respected examples of public private key encryption are RSA, DSS (Digital Signature Standard) and various elliptic curve techniques. The default key file name depends on the algorithm, in this case idrsa when using the default RSA algorithm. It could also be, for example, iddsa or idecdsa. Then it asks to enter a passphrase. The passphrase is used for encrypting the key, so that it cannot be used even if someone obtains the private key file. Dec 30, 2016 PKI enables internet users to exchange information in a secure way with the use of a public and private key. Key Size and Algorithms There are RSA, DSA, ECC ( Elliptic Curve Cryptography ) algorithms that are used to create a public and private key in public key cryptography (Asymmetric encryption). Asymmetric algorithms require the creation of a public key and a private key. The public key can be made public to anyone, while the private key must known only by the party who will decrypt the data encrypted with the public key. This section describes how to generate and manage keys for both symmetric and asymmetric algorithms. Symmetric Keys.

• Algorithms For Generating Private Key West
• Domain Generating Algorithm

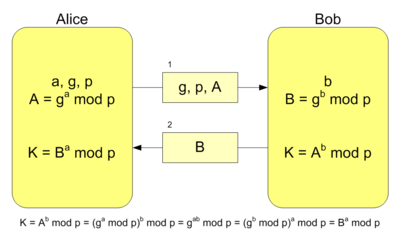
RSA(Rivest-Shamir-Adleman) is an Asymmetric encryption technique that uses two different keys as public and private keys to perform the encryption and decryption. With RSA, you can encrypt sensitive information with a public key and a matching private key is used to decrypt the encrypted message. Asymmetric encryption is mostly used when there are 2 different endpoints are involved such as VPN client and server, SSH, etc.

Below is an online tool to perform RSA encryption and decryption as a RSA calculator.

For Java implementation of RSA, you can follow this article.

First, we require public and private keys for RSA encryption and decryption. Hence, below is the tool to generate RSA key online. It generates RSA public key as well as the private key of size 512 bit, 1024 bit, 2048 bit, 3072 bit and 4096 bit with Base64 encoded.

By default, the private key is generated in PKCS#8 format and the public key is generated in X.509 format.

Generate RSA Key Online

RSA Encryption and Decryption Online

Below is the tool for encryption and decryption. Either you can use the public/private keys generated above or supply your own public/private keys.

Any private or public key value that you enter or we generate is not stored on this site, this tool is provided via an HTTPS URL to ensure that private keys cannot be stolen.

This tool provides flexibility for RSA encrypt with public key as well as private key along with RSA decrypt with public or private key.

If You Appreciate What We Do Here On Devglan, You Can Consider:

• Like us at: or follow us at
• Share this article on social media or with your teammates.
• We are thankful for your never ending support.

Usage Guide - RSA Encryption and Decryption Online

In the first section of this tool, you can generate public or private keys. To do so, select the RSA key size among 515, 1024, 2048 and 4096 bit click on the button. This will generate the keys for you.

For encryption and decryption, enter the plain text and supply the key. As the encryption can be done using both the keys, you need to tell the tool about the key type that you have supplied with the help of radio button. By default, public key is selected. Then, you can use the cipher type to be used for the encryption. The different cipger options are RSA, RSA/ECB/PKCS1Padding and RSA/ECB/OAEPWithSHA-1AndMGF1Padding. Now, once you click the encrypt button the encrypted result will be shown in the textarea just below the button.

Remember, the encrypted result is by default base64 encoded.

Similarly, for decryption the process is same. Here, you need to enter the RSA encrypted text and the result will be a plain-text. You have both options to decrypt the encryption with public and private keys.

• References

Please enable JavaScript to view the comments powered by Disqus.

It’s common knowledge today that a blockchain is a form of a distributed ledger that holds transactions. These transactions are collected in a block and added to the ledger with a reference to the previous block by means of hashes so that a block, once added, can no longer be changed. Well, in theory, a block could change, but given the computing power necessary to calculate a hash for a block and the fact that blockchain is distributed it’s extremely difficult. You would need to have 51% of the computing power to do so (https://learncryptography.com/cryptocurrency/51-attack).

This process of calculating a hash for a block is one part in keeping the blockchain trusted. However, what is stopping users from submitting transactions on funds that they don’t actually own? How is it, that I cannot simply publish a transaction that says “transfer 1000 of this cryptocurrency to someone else”.

To understand what’s stopping us from doing so, we need to look at a second part of blockchain technology: public/private key pairs and using them for signatures.

We will be using C# code and .NET Core to work our way through this concept.

Public/private key pair

Asymmetrical cryptography is a technique that uses pairs of keys:

1. A public key, visible to anyone.
2. A private key, only known to the owner.

The private key is essentially a randomly generated number. The public key can be derived from that public key using what’s called Elliptic Curve Cryptography. We can use ECC for encryption, digital signatures, pseudo-random generators and other tasks. Bitcoin uses a specific elliptic curve called secp256k1 over the finite (prime) field of (2²⁵⁶-2³²-2⁹-2⁸-2⁷-2⁶-2⁴-1) number of elements, using the generator point (on the curve) G=(x, y) where (in hexadecimal):

x=79be667ef9dcbbac55a06295ce870b07029bfcdb2dce28d959f2815b16f81798
y=483ada7726a3c4655da4fbfc0e1108a8fd17b448a68554199c47d08ffb10d4b8

Don’t worry, we will not dive any further into the mathematical details of these ECC algorithms. If you want to know more, check out this article: https://eng.paxos.com/blockchain-101-elliptic-curve-cryptography

In simple code, this is what we do to get the public key from a (random) private key:

The method GetPublicKeyFromPrivateKey looks like this:

The classes CurveFp and Point can be found in the Github repository for this article: https://github.com/sander-/working-with-digital-signatures

If you run this code, you will get following output:

Obviously, having 123456789 as a private key is not particularly safe. But from the public key, there is no way to derive the value of the private key.

Signatures

Algorithms For Generating Private Key West

The process of signing a message entails that you generate a hash that is based on your private key. As you know, hashing is a one-way process, so there’s no way to derive the private key from this hash. However, it is possible to verify whether this hash is accurate if you have the public key of the signer. A digital signature scheme typically consists of 3 algorithms:

1. A key generation algorithm that selects a private key uniformly at random from a set of possible private keys. The algorithm outputs the private key and a corresponding public key.
2. A signing algorithm that, given a message and a private key, produces a signature.
3. A signature verifying algorithm that, given the message, public key and signature, either accepts or rejects the message’s claim to authenticity.

In blockchain, the signature algorithm is the Elliptic Curve Digital Signature Algorithm or ECDSA (https://en.wikipedia.org/wiki/Elliptic_Curve_Digital_Signature_Algorithm). We are not diving into the mathematics of this algorithm. We are, however, going to borrow functions from the BouncyCastle framework (https://www.bouncycastle.org/) to work with ECDSA.

Domain Generating Algorithm

The steps to create a signature for a message are simple.

1. Write the message to be signed.
2. Create a public/private key pair; to generate the public key from the private key we use the secp256k1 algorithm from before.
3. Generate the signature for the message using a signer object.

Strictly speaking, to sign a message we only need a private key. However, signing a message and not giving anyone the public key to verify the signature is pretty pointless.

In code, that reads as follows.

Let’s first look at our new method for generating a public key.

Malwarebytes license key and id generator. For the sake of readability, the return value of the method is base58 encoded (https://en.wikipedia.org/wiki/Base58).

If we call this method we get our public key, based on the private key we gave as input. Ssh key generation in centos. So, our public/private key pair contains these values respectively:

The method GetSignature is this.

The outcome of this method is again base58 encoded to make it easier to read.

We can pass this message signature to someone else. The other party will obviously not have the private key to recreate that signature. But we can also publish the public key and thereby allow the other party to do two things.

1. The other party can verify that the message was signed by the keeper of the private key that belongs to or pairs with the public key.
2. The other party can also verify that the message was not changed by someone else that didn’t have this private key.

Either a change in the message or in the public key would immediately be recognized as the signature would no longer match. Only the original creator of the message together with his private key can make it so the signature is valid.

To verify the signature, we use this code.

As you can see, nowhere do we specify the private key. The BouncyCastle framework does most if not all of the heavy lifting here in providing a signer object that uses ECDSA.

Transactions in the blockchain

The fact that we can have messages from a known source and that these messages cannot be altered by a third party is essential to transactions in a blockchain. Instead of an unstructured message, transactions have a clear structure. This structure looks something like this:

The From and To properties of the transaction are not simple addresses. They are public keys that help verify the sender and the content of the transaction. The transaction and its signature can be created like this.

Following this code, you can see that the message is signed by the owner of the private key that pairs with the public key. By verifying the signature, you can prove that:

1. The creator of the transaction is the holder of the private key belonging to the sender/creator of the transaction.
2. The receiver is the original intended receiver.
3. The amount has not been altered.

Changing any of the parameters (FromPublicKey, ToPublicKey or Amount) would invalidate the signature and therefore make the entire transaction invalid. Verifying the transaction is simple.

In summary

Signing is a good way to know something is being done by the correct person. This means we can trust that someone is actually doing what they say they are. In the real world signatures can be faked. The digital ones cannot. Digital signatures act like electronic “fingerprints.” In the form of a coded message, the digital signature securely associates a signer with a message in a recorded transaction. If you want to know person A sent something, make them sign it before moving forward. If there’s any dispute, check the signature. This is a vital part of the blockchain.

The source code for this post can be found at: https://github.com/sander-/working-with-digital-signatures.